什么是二叉搜索树

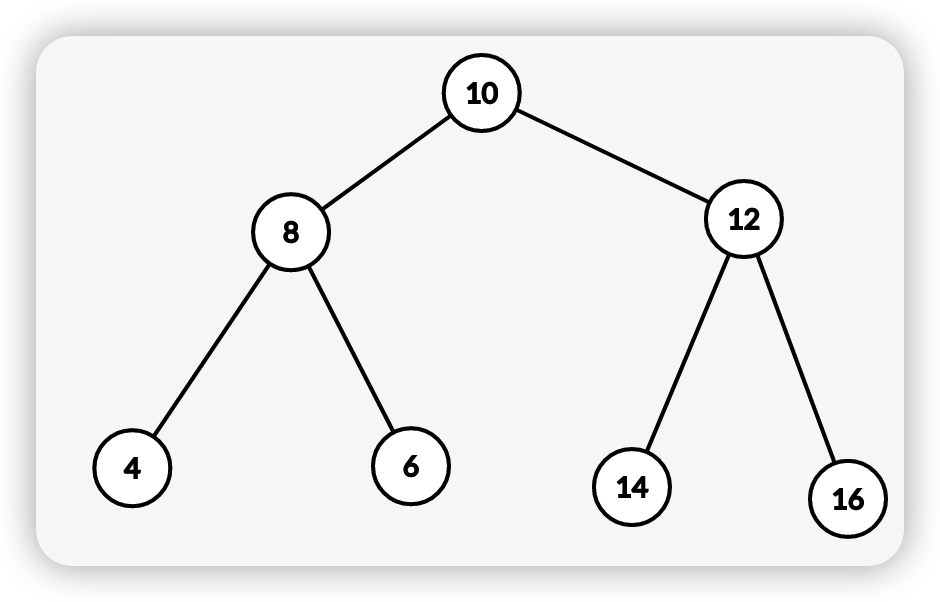
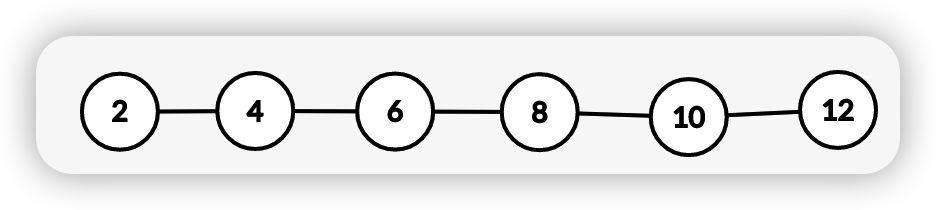
二叉搜索树(binary search tree)是一种具有以下性质的二叉树(假设树不为空)：
1.若其左子树不为空，则其左子树的所有节点的值都小于其根节点的值
2.若其右子树不为空，则其右子树的所有节点的值都大于其根节点的值
3.若将其中的任意一个节点视为根节点的左右子树也都为二叉搜索树

因为二叉搜索树具有上述的特点，因此如果我们需要查找其中的一个值时，若该值小于当前节点的值则向左遍历，若该值大于当前节点的值则向右遍历，从而可以快速地查找到所需要的值。这种分治的方法类似于数组中的二分查找，而不是从头开始依次遍历，暴力查找所需的值，因此查找效率较高。另外，由于二叉搜索树是一种非线性的链式结构，因此也像链表一样，增加和删除效率也很高。

二叉搜索树的时间复杂度

对于普通的二叉搜索树而言，无论是进行增删改查中的哪一种方式，时间复杂度最低都是 O(log n) ，最高都是 O(n)。理由如下：
假设该二叉树是一种平衡二叉树（即长度最长的叶子节点与长度最短的叶子节点的高度差小于或等于1），比如下方这种情况，那么增删改查的效率最高，为O(log n)。(见下方图1)
但假设该二叉树极度不平衡，那么左子树和右子树的高度相差就会很大，严重情况下甚至能退化成链表。这样的话增删改查的时间复杂度最高会降低至O(n)(类似于数组的暴力搜索)。(见下方图2)

二叉搜索树的建树

二叉搜索树是二叉树的一种，因此我们首先先对树的节点进行定义。每个节点应该具有左节点的指针，右节点的指针，当前节点的值以及当前节点的构造函数。

struct TreeNode
{
    TreeNode* left;
    TreeNode* right;
    int val;
    TreeNode(int x):left(nullptr),right(nullptr),val(x){}
};

我们定义一个bst类并且新增一个init函数用于树的初始构建。这个函数接受一个vector数组，然后依次遍历完成树的构建。如果数组为空，那么返回空指针，否则依次调用add函数将数组中的每个元素添加到树中(add函数的实现会在下方写出)。构建完成后，返回指向根节点的指针。

    TreeNode* init(vector<int> &nums)
    {
        if(nums.empty()==true)
        {
            return nullptr;
        }
        //创建根节点
        TreeNode*root=new TreeNode(nums[0]);
        //循环遍历将数组中的数加入树中
        for(int cptime=2;cptime<=nums.size();cptime++)
        {
            add(root,nums[cptime-1]);
        }
        //存储根节点
        bst::root=root;
        //返回根节点
        return root;
    }

假设我们使用用例 63 39 97 29 86 99 5 61 建树，形成的结构如下图所示：

根节点的封装

我们在建树的过程中返回并存储了根节点的指针。并且我们将根节点的指针存储到了类中的root变量中，而root是一个私有成员变量，我们并不能在类外手动地去修改它，这样可以防止手动修改导致的一些问题。

private:
    //存储根节点
    TreeNode* root;

如果我们在后方进行增删改查时需要获取根节点，我们可以设计一个公共函数来获取它。

public:
    //获取根节点
    TreeNode* Getroot()
    {
        return bst::root;
    }

二叉搜索树的新增

我们声明一个add函数用于执行二叉树的新增操作，这个函数需要接受二叉树的根节点和需要插入二叉树的值。

    bool add(TreeNode* node,int value)
    {}

由于二叉搜索树中的各个节点的值各不相同，因此在设计函数时，如果插入的值在二叉树中已经存在，则直接返回，不进行新数据的插入。（返回值可以设计成一个bool函数，当进行这种操作时，返回false，使函数的调用者知晓新的值已存在于树中，因此不进行插入操作。其它正常插入的情况则返回true）。
我们在执行插入操作时，要保证插入完成后继续满足二叉搜索树的三种性质。因此，我们不能在二叉搜索树的中间位置或根节点（假设根节点已存在）执行插入操作，因为这样会破坏二叉搜索树原有的结构，这意味着我们只能在二叉搜索树的叶子节点插入元素。
要找到插入节点的合适位置，我们首先要将需要插入的值与根节点作比较，如果这个值小于根节点，则将这个值与根节点的左节点作比较，假设这个值又比根节点的左节点大，我们就继续往根节点的左节点的右节点遍历，以此类推，直到找到一个合适的空节点，我们将其放置在这个位置上，并且使其父节点的指针指向它，并且进行返回操作。

    //新增操作，手动调用请传入根节点，递归可传入其它节点
    bool add(TreeNode* node,int value)
    {
        if(value==node->val)
        {
            //传入相同值，不符合二叉搜索树定义
            return false;
        }
        else if(value<node->val)
        {
            if(node->left==nullptr)
            {
                TreeNode* tree=new TreeNode(value);
                node->left=tree;
                return true;
            }
            else
            {
                add(node->left,value);
                return true;
            }
        }
        else if(value>node->val)
        {
            if(node->right==nullptr)
            {
                TreeNode* tree=new TreeNode(value);
                node->right=tree;
                return true;
            }
            else
            {
                add(node->right,value);
                return true;
            }
        }
    }

我们在每次比较完成后调用函数本身再进行比较的方法叫做递归。因为无论将二叉搜索树的哪个节点再视为根节点，所形成的树也都是一颗二叉搜索树。因此当需要插入的值大于或小于当前节点的值时，我们可以将当前节点的左节点或右节点的指针传入add函数中，来继续向下寻找可插入该值的位置，找到后则通过return一层层地跳出这个嵌套结构。由于在递归过程中，我们调用add函数时都需要传入一个用于和所需要插入的值作比较的节点，因此在我们手动调用该函数时也需要传入树的根节点。如果我们需要在手动调用时不需要传入根节点，那我们可以设计一个在public:下的add函数用于手动调用，然后这个add函数再调用private:下的add_sort函数，这个函数的设计与上面的设计相同。在递归过程中让add_sort函数调用自己，完成插入操作后再逐步返回。这是一种更安全规范的方法。

二叉搜索树的查找

在查找算法的声明上，我们可以依旧参考新增函数的设计，接受一个根节点和一个需要查找的值，然后按照递归的方法来查找这个值。在返回值的类型方面，通常情况下设计成指向查找到的节点的指针。但为了提高函数的复用性，我们将其设计成从栈底到栈顶依次包含从根节点到该节点所有路径的节点的指针的栈。这样当我们在使用其它函数调用这个查找函数时，就可以很轻易地找到它的父节点来进行一些调整。

    //查询操作，返回查询到节点的指针的栈，手动调用请传入根节点
    //栈底:根节点 栈顶:子节点(如果根节点或子节点不存在则栈顶为nullptr)
    stack<TreeNode*> search(TreeNode* node,int value)
    {
        stack<TreeNode*> st;
        search_algo(node,value,st);
        return st;
    }
    //查询算法底层实现
    void search_algo(TreeNode* node,int value,stack<TreeNode*> &st)
    {
        st.push(node);
        if(node==nullptr)
        {
            return;
        }
        else if(node->val==value)
        {
            return;
        }
        else if(value<node->val)
        {
            search_algo(node->left,value,st);
            return;
        }
        else if(value>node->val)
        {
            search_algo(node->right,value,st);
            return;
        }
    }

注意在函数的声明中将栈以引用的方式传入，否则在递归过程中栈将不能被正确构建。

中序遍历的有序性

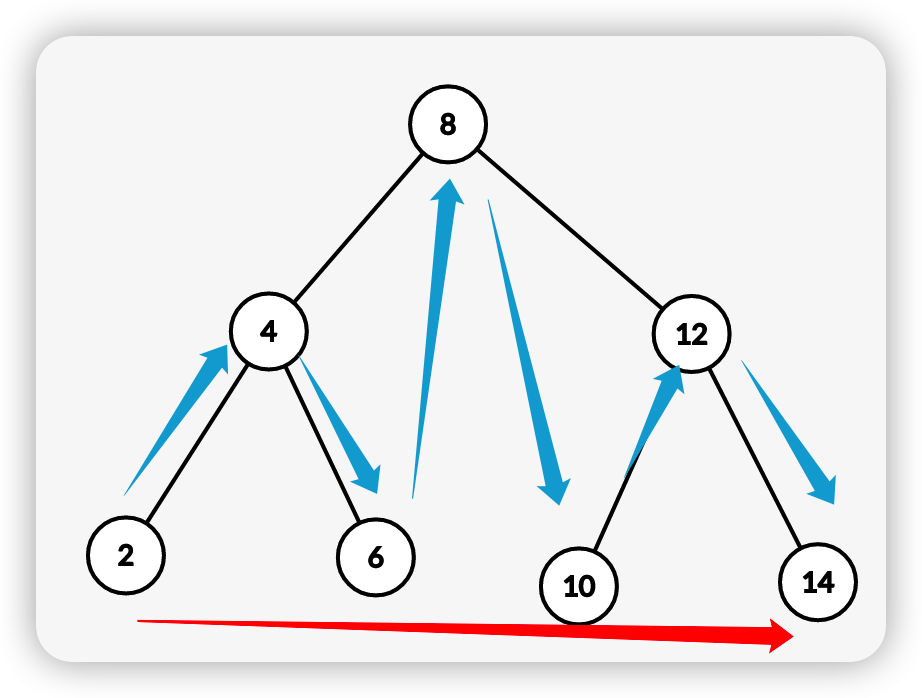
如果说建树是将含有树节点的数组转换为二叉搜索树的结构，那么遍历则是这种操作的反向操作。树的遍历有四种方法，分别是前序遍历，中序遍历，后序遍历，层序遍历，而中序遍历则是按照 左子树->根节点->右子树的顺序将树转换为数组。由于在建树过程中较小的数总是会向左子树构建，而较大的数总是会向右子树构建，因此在中序遍历的过程中，形成的数组也是一种从小到大升序排列的有序结构，示意图如下：

    //中序遍历
    void inorder(TreeNode*node,vector<int> &nums)
    {
        if(node==nullptr)
        {
            return;
        }
        inorder(node->left,nums);
        nums.push_back(node->val);
        inorder(node->right,nums);
    }

删除度为0的节点

我们声明一个函数用于树的删除操作，并且分为度为0，1，2三种情况进行处理。（度指的是该节点拥有的子节点的数量，最小为0，最大为2，假设该节点的左右节点指针都为空，那么度就为0，如果该节点的左右节点指针都不为空，那么度就为2）
接下来我们对度为0的节点的情况进行处理:
度为0意味着该节点的左右指针都为空，那么这个节点必然是二叉搜索树的叶子节点或者单一的根节点。如果该节点是叶子节点，则删除该节点不会对其它节点造成任何影响，因此我们直接将这个节点删除并且将父节点指向这个节点的指针设为空指针即可。如果该节点是单一的根节点，那么我们就需要将该根节点设为nullptr，因为删除该节点后，这棵树将成为一个空树。

在删除叶子节点时必须要将父节点指向这个节点的指针设为nullptr，否则删除该节点后，父节点的指针将继续指向原来该节点的所在的内存，在以后执行诸如查询操作时，强制地访问该内存将会导致程序崩溃 😨。对于如何找到节点的父节点，因为我们在设计查询该节点的函数时使用了栈来存储路径，因此可以轻易地通过将该节点出栈的方式来找到父节点，否则就需要自行编写一套算法来找到父节点。

        //传入不存在的根节点或者未找到相应元素执行的操作
        if(s_value.top()==nullptr)
        {
            return false;
        }
        //度为0的节点执行的操作
        else if(s_value.top()->left==nullptr && s_value.top()->right==nullptr)
        {
            if(is_root==true)
            {
                s_value.top()= nullptr;
            }
            else
            {
                TreeNode* tmp=s_value.top();
                s_value.pop();
                if(s_value.top()->left==tmp)
                {
                    delete tmp;
                    s_value.top()->left=nullptr;
                }
                else
                {
                    delete tmp;
                    s_value.top()->right=nullptr;
                }
            }
            return true;
        }

删除度为1的节点

对于度为1的节点，同样也要分为两种情况：要删除的节点是根节点或不为根节点。如果是根节点的话，我们需要在删除该节点后，将其子节点设为根节点。如果不是根节点，则直接将其父节点的指向该节点的指针指向其子节点并且删除该节点即可。因为如果其父节点的右指针指向该节点，代表该节点的数值大于其父节点的数值，而即使该节点的左指针指向了一个小于该节点的值，那么这个值也是一定大于其父节点的父节点的值的，否则拥有这个值的节点不会作为其父节点的父节点的右子树中的一个节点，而应该成为其父节点的父节点的左子树的一个节点。综上所述，直接将我们要删除的节点的父节点直接指向其子节点并且删除该节点是正确的。

        //度为1的节点执行的操作
        else if((s_value.top()->left==nullptr) != (s_value.top()->right==nullptr))
        {
            if(is_root==true)
            {
                if(s_value.top()->left!=nullptr)
                {
                    bst::root=s_value.top()->left;
                    delete s_value.top();
                }
                else
                {
                    bst::root=s_value.top()->right;
                    delete s_value.top();
                }
            }
            else
            {
                TreeNode* grandparent=nullptr;
                TreeNode* parent=nullptr;
                TreeNode* son=nullptr;
                parent=s_value.top();
                s_value.pop();
                grandparent=s_value.top();
                if(parent->left!=nullptr)
                {
                    son=parent->left;
                }
                else
                {
                    son=parent->right;
                }
                //非法操作，直接返回
                if(parent->val==grandparent->val)
                {
                    return false;
                }
                else if(parent->val<grandparent->val)
                {
                    grandparent->left=son;
                    delete parent;
                }
                else if(parent->val>grandparent->val)
                {
                    grandparent->right=son;
                    delete parent;
                }
            }
            return true;
        }

删除度为2的节点

删除方法简介

要删除度为2的节点，我们需要考虑删除对该节点的左子树和右子树的影响，不需要考虑对该节点的父节点以上的节点的影响，因为假设需要删除的节点是其父节点的右子树的根节点，我们将需要删除的节点的左右子树中的任意一个节点当作该节点，它的值都是比需要删除的节点的父节点的值要大的。基于这个特点，我们可以分为两种情况：将需要删除的节点的左子树中的最大值的节点移动到该位置并删除需要删除的节点或者将需要删除的节点右子树中的最小值的节点移动到该位置并删除需要删除的节点。

删除方法的随机获取

度为2的节点删除方法有两种，对于具体采用哪种方法，我们可以在每次要执行删除操作时通过生成一个0或1的随机数来实现，这样在经过多轮删除后，二叉搜索树可以尽可能地保持平衡，而不是逐渐向一个固定的方向倾斜并退化。

            //生成随机数，用于后方方法的选择
            mt19937 ge(random_device{}());
            bernoulli_distribution bd(0.5);
            bool way=bd(ge);

这种生成随机数的方法利用了梅森旋转算法作为生成器的算法并且使用伯努利分布来限制生成随机数的范围，这是在c++11中新引入的一种方法。相比于直接使用时间戳来生成随机数的经典方法( srand(); rand(time (0)); )而言，虽然生成的也是一种伪随机数，但其随机性更强。如果你的编译器报错，请检查你的编译器是否支持c++11标准。相关资料：https://zh.cppreference.com/w/cpp/header/random

获取所有节点的值

在选择完删除的方法后，我们需要找到可以替代这个待删除的节点的值。比如我们采用利用右子树中的最小值替代待删除的节点的方法，那我们就需要找到右子树的最小值。我们前面提到过二叉搜索树的中序遍历是有序的，因此我们可以通过中序遍历来获取到树中所有元素的值，然后找到待删除的值的下一个值即可。

            //获得中序遍历数组
vector<int> vec_search;
inorder(bst::root,vec_search);

删除元素

在找到用于替代待删除的节点的值后，我们将那个用于替代的值的节点删除（同样递归调用删除函数来删除那个节点），然后将待删除的节点的值设为用于替代的节点的值。

        //度为2的节点执行的操作
        else if(s_value.top()->left!=nullptr && s_value.top()->right!=nullptr)
        {
            //生成随机数，用于后方方法的选择
            mt19937 ge(random_device{}());
            bernoulli_distribution bd(0.5);
            bool way=bd(ge);
            //获得中序遍历数组
            vector<int> vec_search;
            inorder(bst::root,vec_search);
            //将当前节点替换为左子树最大节点
            if(way==1)
            {
                int node_index= distance(vec_search.begin(),find(vec_search.begin(),vec_search.end(),s_value.top()->val));
                bst::remove(bst::root,vec_search[node_index-1]);
                s_value.top()->val=vec_search[node_index-1];
            }
            //将当前节点替换为右子树最小节点
            else
            {
                int node_index=distance(vec_search.begin(),find(vec_search.begin(),vec_search.end(),s_value.top()->val));
                bst::remove(bst::root,vec_search[node_index+1]);
                s_value.top()->val=vec_search[node_index+1];
            }
            return true;
        }

二叉搜索树的修改

要修改二叉搜索树的值，只需要调用删除函数删除旧的值，然后调用新增函数来增加新的值即可。

    //修改节点，手动调用请传入根节点
    bool edit(TreeNode*node,int old_val,int new_val)
    {
        if(bst::remove(node,old_val)==false)
        {
            return false;
        }
        if(bst::add(node,new_val)==false)
        {
            return false;
        }
        return true;
    }

完整代码

//二叉搜索树
#include <vector>
#include <stack>
#include <random>
#include <iterator>
#include <algorithm>
#include <iostream>
using namespace std;

struct TreeNode
{
    TreeNode* left;
    TreeNode* right;
    int val;
    TreeNode(int x):left(nullptr),right(nullptr),val(x){}
};

class bst{
public:
    //初始化返回根节点
    TreeNode* init(vector<int> &nums)
    {
        if(nums.empty()==true)
        {
            return nullptr;
        }
        //创建根节点
        TreeNode*root=new TreeNode(nums[0]);
        //循环遍历将数组中的数加入树中
        for(int cptime=2;cptime<=nums.size();cptime++)
        {
            add(root,nums[cptime-1]);
        }
        //存储根节点
        bst::root=root;
        //返回根节点
        return root;
    }

    //新增操作，手动调用请传入根节点，递归可传入其它节点
    bool add(TreeNode* node,int value)
    {
        if(value==node->val)
        {
            //传入相同值，不符合二叉搜索树定义
            return false;
        }
        else if(value<node->val)
        {
            if(node->left==nullptr)
            {
                TreeNode* tree=new TreeNode(value);
                node->left=tree;
                return true;
            }
            else
            {
                add(node->left,value);
                return true;
            }
        }
        else if(value>node->val)
        {
            if(node->right==nullptr)
            {
                TreeNode* tree=new TreeNode(value);
                node->right=tree;
                return true;
            }
            else
            {
                add(node->right,value);
                return true;
            }
        }
    }

    //查询操作，返回查询到节点的指针的栈，手动调用请传入根节点
    //栈底:根节点 栈顶:子节点(如果根节点或子节点不存在则栈顶为nullptr)
    stack<TreeNode*> search(TreeNode* node,int value)
    {
        stack<TreeNode*> st;
        search_algo(node,value,st);
        return st;
    }

    //删除操作，手动调用请传入根节点
    bool remove(TreeNode*node,int value)
    {
        stack<TreeNode*> s_value = search(node,value);
        bool is_root=s_value.size()==1? true:false;
        //传入不存在的根节点或者未找到相应元素执行的操作
        if(s_value.top()==nullptr)
        {
            return false;
        }
        //度为0的节点执行的操作
        else if(s_value.top()->left==nullptr && s_value.top()->right==nullptr)
        {
            if(is_root==true)
            {
                s_value.top()= nullptr;
            }
            else
            {
                TreeNode* tmp=s_value.top();
                s_value.pop();
                if(s_value.top()->left==tmp)
                {
                    delete tmp;
                    s_value.top()->left=nullptr;
                }
                else
                {
                    delete tmp;
                    s_value.top()->right=nullptr;
                }
            }
            return true;
        }
        //度为1的节点执行的操作
        else if((s_value.top()->left==nullptr) != (s_value.top()->right==nullptr))
        {
            if(is_root==true)
            {
                if(s_value.top()->left!=nullptr)
                {
                    bst::root=s_value.top()->left;
                    delete s_value.top();
                }
                else
                {
                    bst::root=s_value.top()->right;
                    delete s_value.top();
                }
            }
            else
            {
                TreeNode* grandparent=nullptr;
                TreeNode* parent=nullptr;
                TreeNode* son=nullptr;
                parent=s_value.top();
                s_value.pop();
                grandparent=s_value.top();
                if(parent->left!=nullptr)
                {
                    son=parent->left;
                }
                else
                {
                    son=parent->right;
                }
                //非法操作，直接返回
                if(parent->val==grandparent->val)
                {
                    return false;
                }
                else if(parent->val<grandparent->val)
                {
                    grandparent->left=son;
                    delete parent;
                }
                else if(parent->val>grandparent->val)
                {
                    grandparent->right=son;
                    delete parent;
                }
            }
            return true;
        }
        //度为2的节点执行的操作
        else if(s_value.top()->left!=nullptr && s_value.top()->right!=nullptr)
        {
            //生成随机数，用于后方方法的选择
            mt19937 ge(random_device{}());
            bernoulli_distribution bd(0.5);
            bool way=bd(ge);
            //获得中序遍历数组
            vector<int> vec_search;
            inorder(bst::root,vec_search);
            //将当前节点替换为左子树最大节点
            if(way==1)
            {
                int node_index= distance(vec_search.begin(),find(vec_search.begin(),vec_search.end(),s_value.top()->val));
                bst::remove(bst::root,vec_search[node_index-1]);
                s_value.top()->val=vec_search[node_index-1];
            }
            //将当前节点替换为右子树最小节点
            else
            {
                int node_index=distance(vec_search.begin(),find(vec_search.begin(),vec_search.end(),s_value.top()->val));
                bst::remove(bst::root,vec_search[node_index+1]);
                s_value.top()->val=vec_search[node_index+1];
            }
            return true;
        }
    }

    //修改节点，手动调用请传入根节点
    bool edit(TreeNode*node,int old_val,int new_val)
    {
        if(bst::remove(node,old_val)==false)
        {
            return false;
        }
        if(bst::add(node,new_val)==false)
        {
            return false;
        }
        return true;
    }

    //获取根节点
    TreeNode* Getroot()
    {
        return bst::root;
    }

    //中序遍历
    void inorder(TreeNode*node,vector<int> &nums)
    {
        if(node==nullptr)
        {
            return;
        }
        inorder(node->left,nums);
        nums.push_back(node->val);
        inorder(node->right,nums);
    }

private:
    //存储根节点
    TreeNode* root;

    //查询算法底层实现
    void search_algo(TreeNode* node,int value,stack<TreeNode*> &st)
    {
        st.push(node);
        if(node==nullptr)
        {
            return;
        }
        else if(node->val==value)
        {
            return;
        }
        else if(value<node->val)
        {
            search_algo(node->left,value,st);
            return;
        }
        else if(value>node->val)
        {
            search_algo(node->right,value,st);
            return;
        }
    }
};