算数基本定理
算数基本定理又叫唯一分解定理,它说明任意大于1的自然数都可以唯一地分解成质数的幂的乘积。对于任意两个满足条件的数a,b,我们可以通过以下公式进行分解: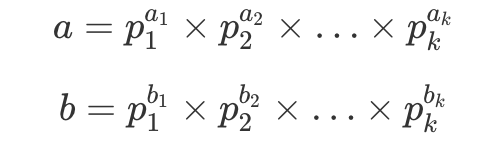
其中p1,p2,....,pk表示质数,而a1,a2,....ak以及b1,b2,...bk表示非负整数。如果一个数拆分成的质数中没有这个质数,可以将幂视作0,比如12=(2^2) (3^1) (5^0) (7^0) .....(后面的7,9,11的幂皆为0)。至于为什么不存在非质数,因为假如将其中的一个非质数视作a的一个因子,那它仍然可以继续拆分成几个质数的乘积(即表示a的式子可以继续化简),经过不断化简,最终得到的式子仍然是所有质数的幂相乘所形成的式子。
最大公约数的数学表示
我们以12和6为例,将这两个数用算数基本定理表示,可以得到以下公式(忽略幂为0的质数因子):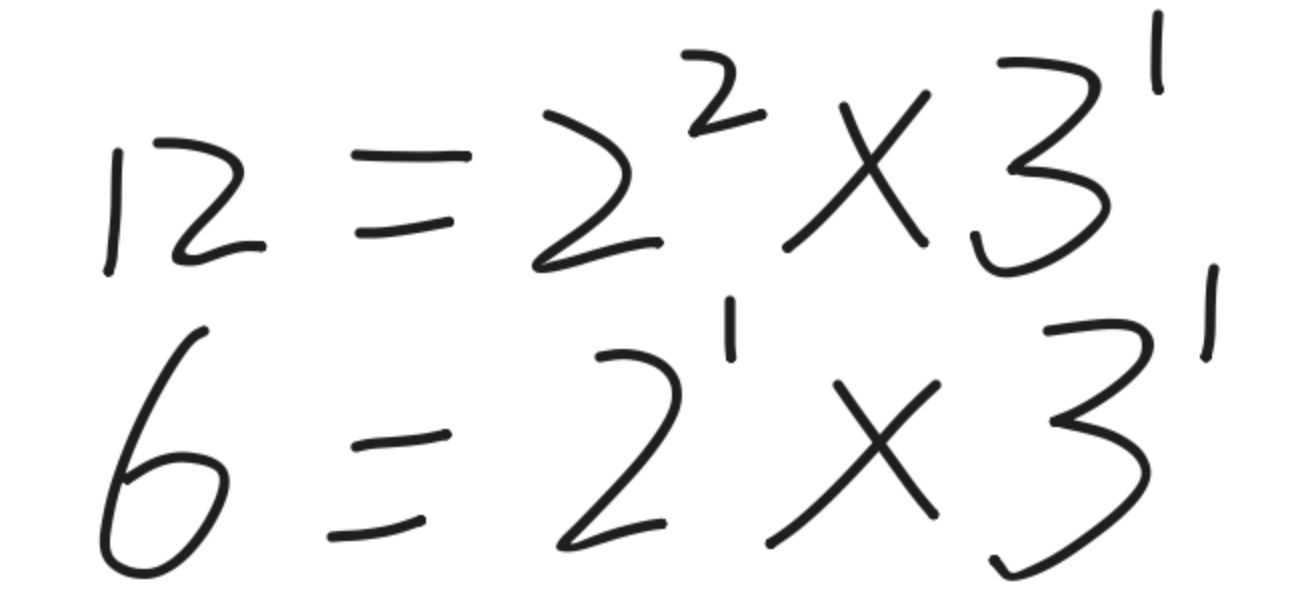
要找到最大公约数,我们就要找到一个共同的数,这个共同的数必须既能将6整除,又能将12整除,而且还必须是最大的。而6和12都可以表示为质数因子2和3的幂的乘积的形式,要找到这个最大的数,我们只需要找到其中 每个因子的最小幂的乘积 即可。寻找最小值是为了保证找到的公约数都能将6和12整除。而寻找每个因子是为了保证这个公约数是最大的(即最大公约数),因为一旦在寻找的过程中遗漏了某个因子,那么就相当于找到的是 用最大公约数除以了这个因子 所得到的数,所以导致找到的这个公约数不是最大的。
根据我们的方法,对于因子2,我们应该寻找的是2的1次方,而对于因子3,我们应该寻找的是3的一次方。将它们相乘,我们得到6和12的最大公约数为2x3=6。
综上所述,对于a,b两个数的最大公约数我们可以这样获得: 将a,b两个数用算数基本定理拆解后,对于相同底数的质数因子,取幂相对较小的那个数,然后将它们相乘,得到的即为a,b的最大公约数
最小公倍数的数学表示
我们仍然以6和12为例,要找到其最小公倍数,即要找到一个既可以被6整除,又可以被12整除的数,并且这个数还要是最小的。根据我们寻找最大公约数的方法,这次我们就应该寻找对于6和12的相同底数的两个因子中较大的那个。这样我们就可以保证了这个数都可以被两个数整除(因为这个数是由两个数的最大因子相乘而得来的,无论用哪个数整除,最终都会将共有的因子除掉,最终得到一个整数)。而且它一定是两个数的最小的公倍数,因为这个数不可以再拆分,如果继续拆分的话,相当于除掉了一个或多个质数,这会导致其无法成为6或者12的一个倍数。(想象一下,我们如果将12和6的最小公倍数12再除以一个2,得到了6,它并不是12的倍数。因为将12拆解后为2的二次方乘以3的一次方,而6拆解后为2的一次方乘以3的一次方,6比12少了一个2的一次方,因此无法成为12的倍数。)
综上所述,对于a,b两个数的最小公倍数我们可以这样获得:综上所述,对于a,b两个数的最大公约数我们可以这样获得: 将a,b两个数用算数基本定理拆解后,对于相同底数的质数因子,取幂相对较大的那个数,然后将它们相乘,得到的即为a,b的最小公倍数
最大公约数和最小公倍数的乘积
我们将a,b的最大公约数视作GCD(a,b),将a,b的最小公倍数视作LCM(a,b)。则可以得到GCD(a,b) x LCM(a,b) = a x b。
推论如下:假设存在 6 和 12,我们将其用算数基本定理进行拆解
6= 2^1(q) x 3^1(t)
12= 2^2(s) x 3^1(d)
6 x 12= 72 = (q) x (t) x (s) x (d)
则GCD(6,12)=2^1(q) x 3^1(d)
LCM(6,12)=2^2(s) x 3^1(t)
则GCD(6,12) x LCM(6,12)= (q) x (t) x (s) x (d) =72=6 x 12
因此,对于a,b而言,GCD(a,b) x LCM(a,b) = a x b。
欧几里得算法
该算法基于以下事实:两个正整数的最大公约数(GCD)不变,即使其中一个数被它们的差替换。
假设存在两个非负正整数a,b且存在a>b而言。GCD(a,b)=GCD(b,a-b)。
证明过程如下:
如果d是a和b的最大公约数,则a=m x d,而b=n x d。(如果你不理解为什么可以这样表示,你需要重新理解前方所提到的知识)
a-b=(m-n)x d。
因此我们可以通过设计算法不断使其相减,最终使得a,b变量的其中一个值变为0,而另外一个值即为我们们要找到的最大公约数。
根据这个原理,我们可以设计两个或者两个以上的数的求最大公约数的算法:
// 最大公约数算法
int gcd(int a, int b)
{
int tmin = min(a, b);
int tmax = max(a, b);
if (tmin != 0)
{
tmax = tmax - tmin;
return gcd(tmin, tmax);
}
return tmax;
}
// 最大公约数算法扩展
int tgcd(int a, int b, int c)
{
return gcd(gcd(a, b), c);
}由于我们已经在上方得到了最大公约数和最小公倍数的乘积与两个数乘积之间的关系,因此我们可以这样设计求两个数最小公倍数的算法:
int lcm(int a,int b)
{
return (a*b/gcd(a,b));
}c++17计算最小公倍数和最大公约数
如果你的编译器支持c++17或更高标准,你可以分别使用lcm()函数和gcd()函数来计算最小公倍数和最大公约数。它包含在头文件numeric下。
详解如下:
https://zh.cppreference.com/w/cpp/numeric/gcd
https://zh.cppreference.com/w/cpp/numeric/lcm
演示代码:
#include <numeric>
using namespace std;
int main()
{
int a=10,b=20;
int j=lcm(10,20);
int k=gcd(10,20);
return 0;
}结果为j=20 k=10。
求最大公约数的改良算法
假如有下面一个问题:
我们将公式S化简可以得到S=gcd(a,b,c)。因此,我们可以设计一个gcd算法进行暴力求解。代码如下:
#include <iostream>
#include <vector>
#include <iterator>
#include <algorithm>
using namespace std;
// 最大公约数算法
int gcd(int a, int b)
{
int tmin = min(a, b);
int tmax = max(a, b);
if (tmin != 0)
{
tmax = tmax - tmin;
return gcd(tmin, tmax);
}
return tmax;
}
// 最大公约数算法扩展
int tgcd(int a, int b, int c)
{
return gcd(gcd(a, b), c);
}
int main()
{
// 获取并加入数组
int n;
cin >> n;
vector<int> diamonds(n, -1);
for (int cptime = 1; cptime <= n; cptime++)
{
cin >> diamonds[cptime - 1];
}
// 组合数学
vector<vector<int>> combinations;
for (int i = 1; i <= diamonds.size() - 2; i++)
{
for (int j = i + 1; j <= diamonds.size() - 1; j++)
{
for (int k = j + 1; k <= diamonds.size(); k++)
{
combinations.push_back({diamonds[i - 1], diamonds[j - 1], diamonds[k - 1]});
}
}
}
// 计算s
vector<int> s;
for (int cptime = 1; cptime <= combinations.size(); cptime++)
{
int a = combinations[cptime - 1][0];
int b = combinations[cptime - 1][1];
int c = combinations[cptime - 1][2];
s.push_back(tgcd(a, b, c));
}
// 寻找最大元素
vector<int>::iterator it;
it = max_element(s.begin(), s.end());
int dis = distance(s.begin(), it);
// 输出
vector<int> sum = {combinations[dis][0], combinations[dis][1], combinations[dis][2]};
sort(sum.begin(), sum.end());
cout << sum[0] << " " << sum[1] << " " << sum[2];
return 0;
}但这存在一个问题。由于我们需要获取到数组中所有可能存在的以三个为一组的组合,因此算法的时间复杂度是O(n^3)。这对于大数据是极其致命的,所以我们需要设计一种更高效的算法。这种算法需要去除获取所有可能的组合的步骤,这是一个三层嵌套循环,正是这个循环让算法的复杂度到了O(n^3)级别。
一种比较好的解决方法如下:我们将每一个数据求出其所有可以被整除的数,并将这个数出现的次数统计下来,哪个数出现的次数等于3,就代表这个数字可以同时整除数组中的三个的数。所有出现次数等于3的数对应的就是题目中的S,而最大的那个数就是S的最大值。有时候一个数字出现的次数也可以大于3,这代表这个数可以将数组中的多个数整除,这时候我们也只需要找出那个最小的组合即可(如题所见,它需要我们找到字典中的最小的那个组合)。这个数字出现的次数可能是4次,5次甚至是6次,但是对于暴力搜索一开始遍历并找出所有可能的组合而言,这种算法的时间复杂度开销要少得很多。
另外值得一提的是,我们在遍历一个数所有可能整除的数字时,我们只需要从1遍历到其二次方根即可,因为对于一个可以被b和c整除的数a而言,总有a=b(小) x c(大)。我们只要遍历出那个比较小的值,另一个比较大的值只需要用a除以这个比较小的值就可以得到了。b和c的分界线是a的平方根,原因在于假设b等于a的平方根时,c也等于a的平方根,当b和c之中的任意一个数再增大时,这个数会变成较大的那个数,所对应的另一个数必定会变成较小的那个数,而这两个数一定是我们在遍历1到a的平方根的过程中已经遍历过的。
综上所述,解决本问题的完整代码如下,本算法的时间复杂度在对数级别:
#include <iostream>
#include <vector>
#include <algorithm>
#include <map>
#include <iterator>
#include <math.h>
using namespace std;
int main()
{
int n;
cin >> n;
vector<int> nums(n, 0);
for (int cptime = 1; cptime <= n; cptime++)
{
cin >> nums[cptime - 1];
}
sort(nums.begin(), nums.end());
// 存储公约数
map<int,vector<int>> m;
// 正式遍历
for (int cptime = 1; cptime <= nums.size(); cptime++)
{
int cur_maxnumber = nums[cptime - 1];
//平方根放缩优化
for (int ncptime = 1; ncptime <= sqrt(cur_maxnumber); ncptime++)
{
if (nums[cptime - 1] % ncptime == 0)
{
m[ncptime].push_back(nums[cptime-1]);
//求较大因数并加入map
int bignumber=nums[cptime-1]/ncptime;
//防止重复项
if(bignumber!=ncptime)
{
m[bignumber].push_back(nums[cptime-1]);
}
}
}
}
// 寻找最大公约数及查找算法
int sumindex = -1;
vector<int> sums(3,-1);
map<int, vector<int>>::iterator it;
for (it=m.begin();it!=m.end();it++)
{
if(it->second.size()>=3)
{
if(it->first>=sumindex)
{
sumindex=it->first;
sums[0]=it->second[0];
sums[1]=it->second[1];
sums[2]=it->second[2];
}
}
}
// 输出答案
sort(sums.begin(),sums.end());
cout<<sums[0]<<" "<<sums[1]<<" "<<sums[2];
return 0;
}