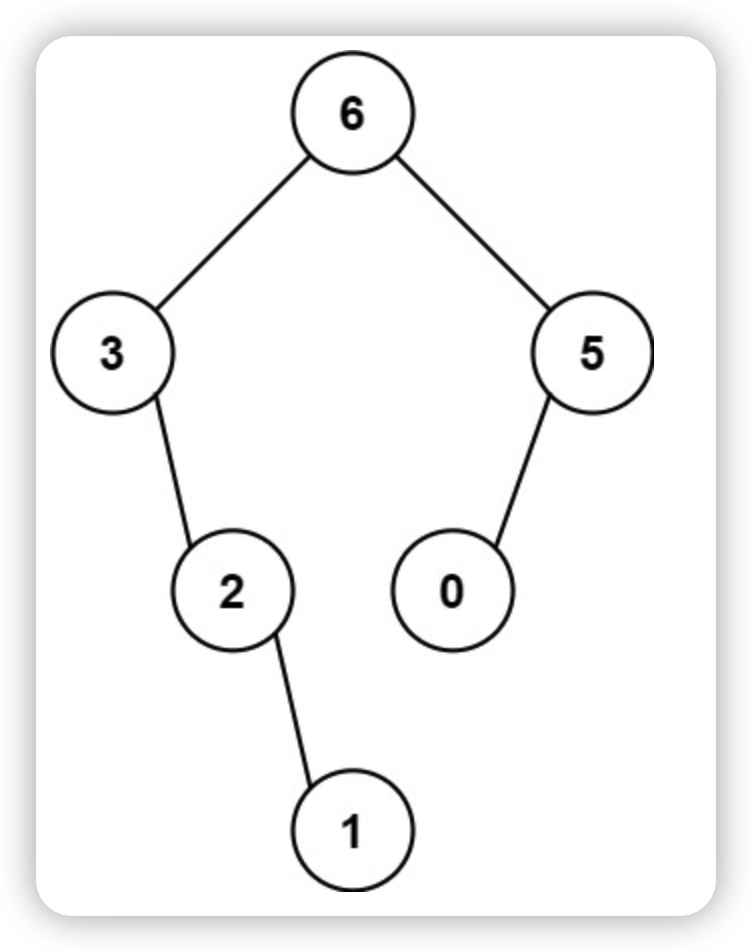
问题简介

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

1.创建一个根节点，其值为 nums 中的最大值。
2.递归地在最大值 左边 的 子数组前缀上 构建左子树。
3.递归地在最大值 右边 的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

提示：
1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同

代码模版

  struct TreeNode {
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      };

class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
    }
};

初步分析——建树

最大二叉树中的子节点的数值总是小于父节点的数值，并且要构建最大二叉树，我们需要找出其中的最大的那一个数作为根节点。这个根节点的左边的最大的数作为根的左子节点，这个根节点右边的最大的数作为根的右子节点作为根的右子节点，以此类推。因此，我们可以维护一个栈。从数组的第一个数开始遍历。如果栈为空，则直接将当前遍历的数直接入栈。如果栈不为空，则考虑下面的情况：
1.如果当前的数小于栈顶的数，则意味着这个数应该作为栈顶的数的右子节点（这个数作为栈顶的右子节点而不作为左子节点的原因在于这个数在数组中的位置一定是在栈顶的数的后方的，因此如果这个数小于栈顶的数，则只能作为栈顶的数的右子节点而不是左子节点），则我们将栈顶的数的右指针指向这个数并且将这个节点压栈。
2.如果当前的数大于栈顶的数，则意味着栈顶的数应该作为这个数的左子节点(也是从这两个数在数组中的位置进行考虑，这个数大于栈顶的数且在栈顶的数的右方，则栈顶的数肯定是这个数的左子节点或者这个数的左子节点的子节点)。因此我们需要将栈顶的数进行出栈，并且让这个数的左子节点指向它。通过不断的出栈并且设置这个数的左子节点，这个数将会指向原来栈中小于这个数但是相对于整个栈而言最大的那个数，也就是栈底的那个节点。完成操作后，原来栈中的元素则会作为这个数左节点，而这个数则作为整个树的根节点，我们将这个树压入栈中。
不断重复这个操作，如果再往后的数满足情况1，则后面的数会作为这棵具有左子节点但不具有右子节点的树的右子节点。如果满足情况2，则这颗树会作为新的树的左子节点。随着遍历的不断进行，最大二叉树就会被不断构建出来。下面是示例一的构建详情：

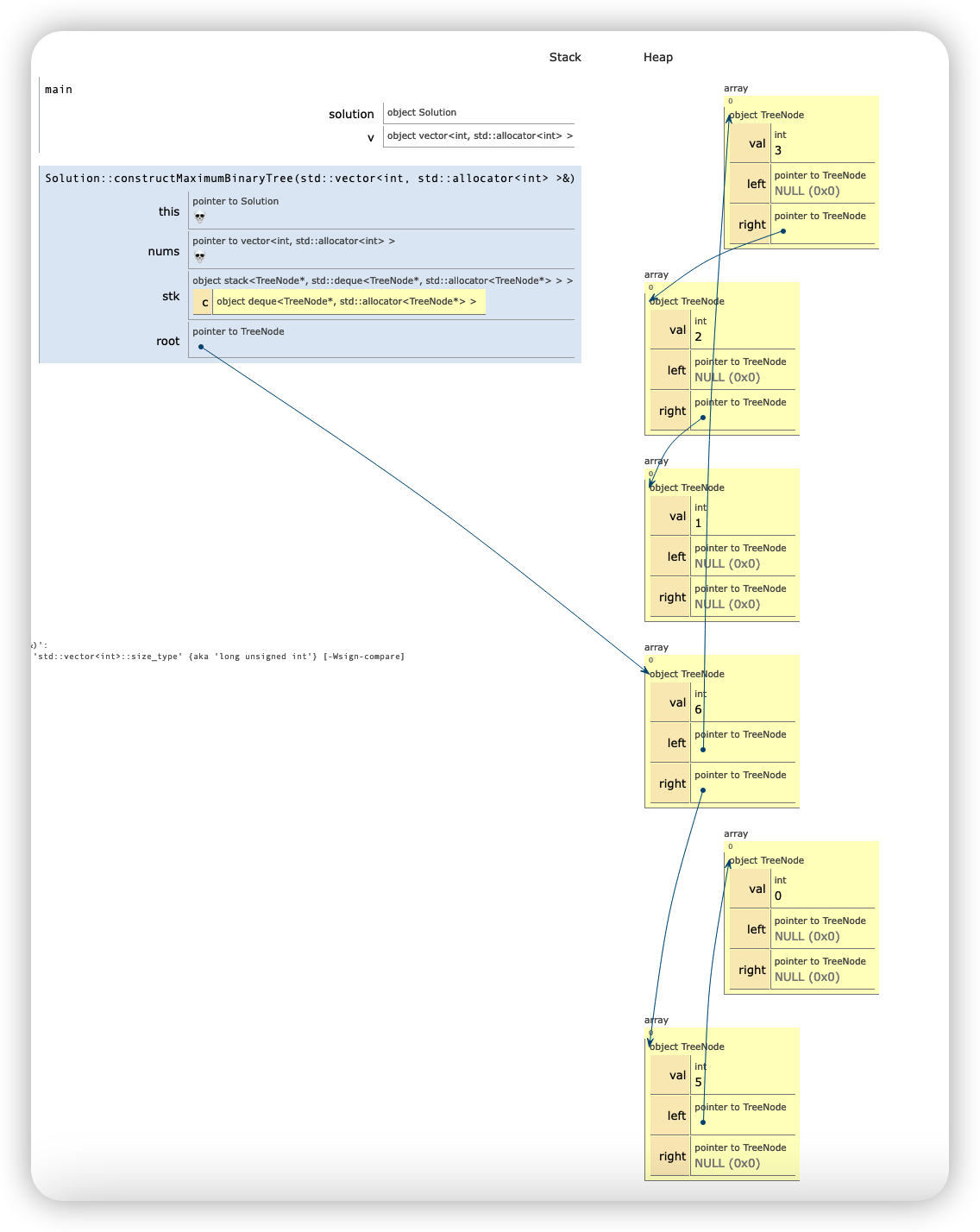
为什么栈底的元素总是栈中最大的元素

在上方建树过程中，一旦我们遍历到的数组中的元素（相对于栈中的元素是较新的数）小于栈顶的元素，则这个数将作为原来的栈顶的数的右节点并且被压入栈中。相反，如果新的数大于栈顶的元素，则这个栈顶的元素会被弹出栈并且作为这个新数的左子节点，然后这个带有原来栈顶元素的新数会被压入栈中。这样使得原来栈顶中小于这个数的元素被弹出了栈，取而代之的是一颗新数作为根节点的树，原来的栈顶元素虽然没有消失，变成了这个新树中的一个左子节点，但当我们后面进行比较时，比较的是在这个栈中的树的根节点的那个数的大小。而作为最大二叉树而言，根节点无疑是最大的那个数，这使得如果在后面继续遍历和比较操作时，比这个数小的数会不断被压入栈中并作为原来比较大的数的右节点，而如果后面一旦有比这个数大的数，原来栈底相对较大的那个数会被弹出栈并作为新的大的树的左子节点，新的大的树会再次入栈，成为栈底元素。通过这种操作，每次新数压栈完成后栈底的元素总是最大的，栈顶的元素总是最小的。这种类似于单增数列或单减数列的具有单调性的栈称为 单调栈 。通过单调栈的应用，我们可以快速地完成最大二叉树的构建过程。相关演示视频如下：

回溯并找到树的根节点

完成数组的遍历操作后我们就完成了整棵树的构建。但我们需要通过回溯来找到整棵树的根节点。最大二叉树的特点在于根节点是整棵树中最大的那个数，而在我们构建的单调栈中，栈底的元素就是最大的那个数。因此我们只需要通过不断的出栈操作，来找到栈底的那个元素所对应的指针，就找到了整棵树的根节点。

最终代码

#include <vector>
#include <stack>
using namespace std;
struct TreeNode {
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      };
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        stack<TreeNode*> stk;
        for(int i=0;i<nums.size();i++)
        {
            TreeNode* cur=new TreeNode(nums[i]);
            while(stk.empty()==false && stk.top()->val<=nums[i])
            {
                cur->left=stk.top();
                stk.pop();
            }
            if(stk.empty()==false)
            {
                stk.top()->right=cur;
            }
            stk.push(cur);
        }
        TreeNode *root=nullptr;
        while(stk.empty()==false)
        {
            root=stk.top();
            stk.pop();
        }
        return root;
    }
};