题目简介

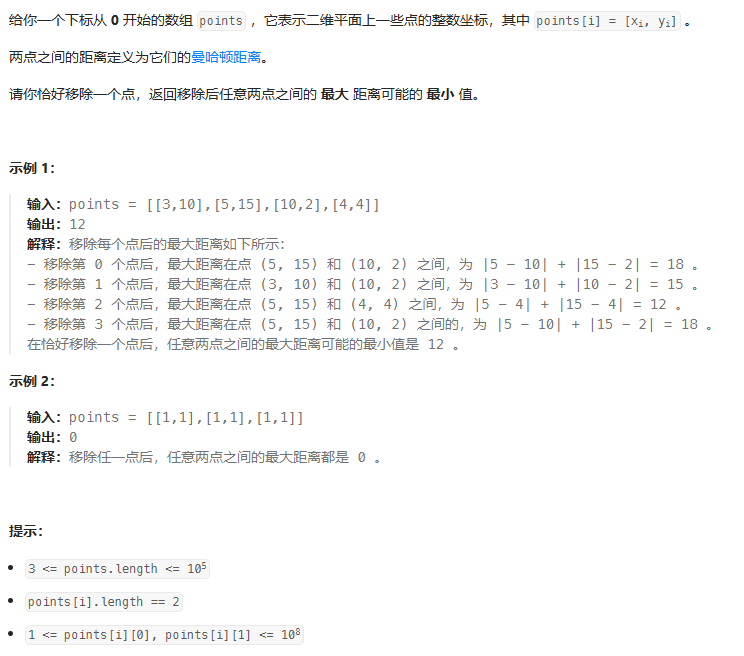
曼哈顿距离的定义：两个单元格 (xi, yi) 和 (xj, yj) 之间的曼哈顿距离为 |xi - xj| + |yi - yj|。

题目分析

由曼哈顿距离的定义可知：若要使用其定义求两个点之间的曼哈顿距离，则要求的两个点的坐标必须是已知的。因此，根据题目要求，我们需要依次枚举（去除）每个点，然后再将剩下的点两两一组，使用定义式来求出它们的曼哈顿距离，然后在这些曼哈顿距离中取一个最小值。枚举完毕后，再在这些"对于每次枚举，求出的曼哈顿距离中的最小值"中再取一次它们的最小值。即可解决本问题。
但细心的你可能会发现，这么做会使得算法的时间复杂度过高，因此我们需要对算法进行优化。我们可以先对曼哈顿距离公式进行化简，化简过程如图所示：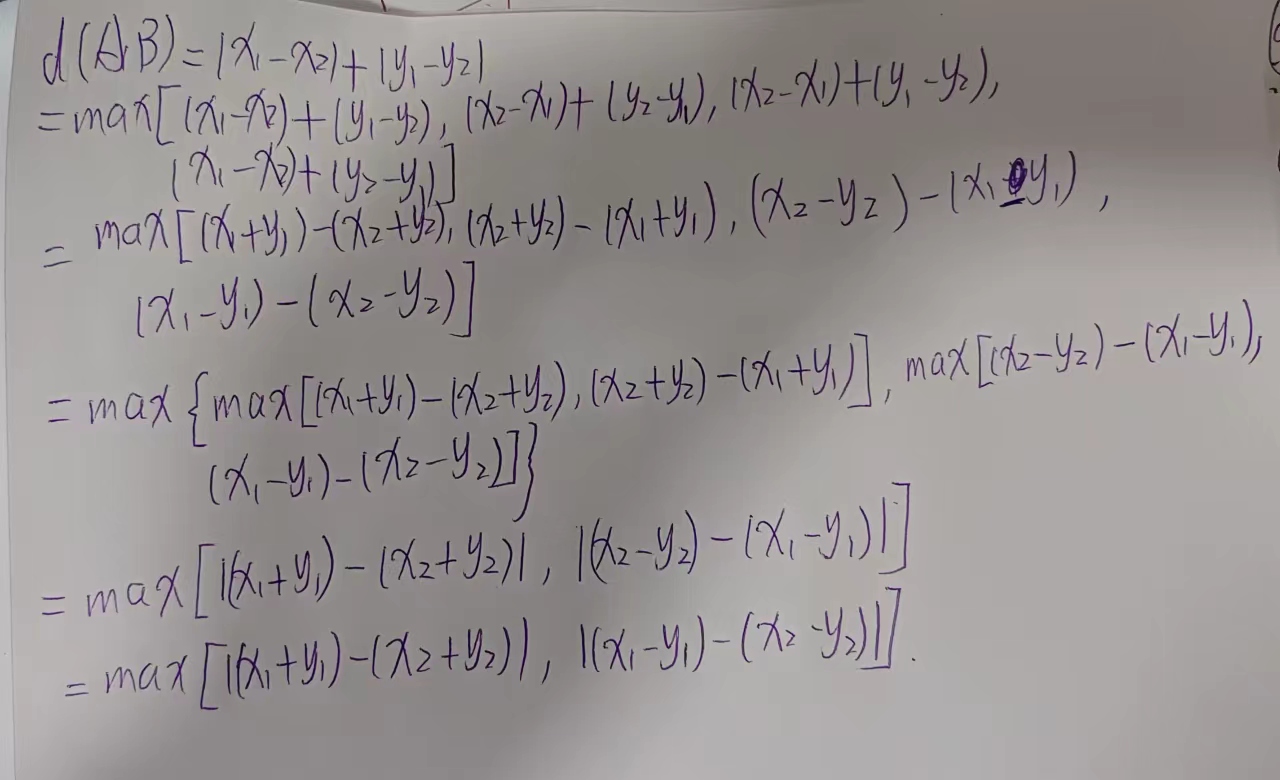

由化简后的式子可知，对于任意两个点的曼哈顿距离，我们可以这样求解：
1.先分别求出每个点的横纵坐标之和 以及 横纵坐标之差
2.将这两个点的横纵坐标之和相减并求绝对值，记作a。将这两个点的横纵坐标之差相减并求绝对值，记作b。
3.求a和b中的最大值，记作c。c即为两点之间的曼哈顿距离。

根据这个原理，我们继续对其化简：

因此，我们可以维护两个数组Sxy1和Sxy2。Sxy1数组存储了所有点的横纵坐标之和，Sxy2数组存储了所有点的横纵坐标之差。如果我们要求曼哈顿距离的最大值，那么只需要 用每个数组的最大值减去最小值，求绝对值，并将求出的两个值取最大值 即可。但根据题目的要求，我们需要求的是移除某个点后的曼哈顿距离的最大值所形成的数组中的最小值。因此，我们需要按照以下步骤来解决问题：

1.枚举每个点，求出其 x+y ，并在Sxy1数组中删除。求出其 x-y，并在Sxy2数组中删除。
2.使用曼哈顿距离公式的推论，求出曼哈顿距离的最大值Q。
3.将Q与之前推出的数（即之前推出的Q）做比较，假设Q小于之前推出的数，则更新结果sum为Q，记作min(Q)。
4.将之前删除的 x+y 和 x-y 重新加入数组中，开始下一个数的枚举。
5.完成所有数的枚举遍历后，返回min(Q)。

值得一提的是，对于Sxy1和Sxy2，之前为了便于讲解，一直强调其为两个数组。实际上，该算法涉及到频繁地对Sxy1和Sxy2进行增删改查，这会降低算法的执行效率。对于C++实现，推荐使用multiset 来进行操作。这是一种基于红黑树的数据结构，在本问题中可以大幅降低算法的时间复杂度。

完整代码实现

#include <vector>
#include <set>
#include <math.h>
using namespace std;

class Solution {
public:
    int minimumDistance(vector<vector<int>>& points) {
        multiset<int> Sxy1,Sxy2;
        for(int cptime=1;cptime<=points.size();cptime++)
        {
            Sxy1.emplace(points[cptime-1][0]+points[cptime-1][1]);
            Sxy2.emplace(points[cptime-1][0]-points[cptime-1][1]);
        }
        int sum=INT_MAX;
        for(int cptime=1;cptime<=points.size();cptime++)
        {
            int j=points[cptime-1][0]+points[cptime-1][1];
            int k=points[cptime-1][0]-points[cptime-1][1];
            Sxy1.erase(Sxy1.find(j));
            Sxy2.erase(Sxy2.find(k));
            int temp_max=max(abs(*(Sxy1.rbegin())-*(Sxy1.begin())),abs(*(Sxy2.rbegin())-*(Sxy2.begin())));
            if(temp_max<=sum)
            {
                sum=temp_max;
            }
            Sxy1.emplace(j);
            Sxy2.emplace(k);
        }
        return sum;
    }
};