Leetcode.622 设计循环队列
设计你的循环队列实现。 循环队列是一种线性数据结构,其操作表现基于 FIFO(先进先出)原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
你的实现应该支持如下操作:
MyCircularQueue(k): 构造器,设置队列长度为 k 。
Front: 从队首获取元素。如果队列为空,返回 -1 。
Rear: 获取队尾元素。如果队列为空,返回 -1 。
enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
isEmpty(): 检查循环队列是否为空。
isFull(): 检查循环队列是否已满。
MyCircularQueue circularQueue = new MyCircularQueue(3); // 设置长度为 3
circularQueue.enQueue(1); // 返回 true
circularQueue.enQueue(2); // 返回 true
circularQueue.enQueue(3); // 返回 true
circularQueue.enQueue(4); // 返回 false,队列已满
circularQueue.Rear(); // 返回 3
circularQueue.isFull(); // 返回 true
circularQueue.deQueue(); // 返回 true
circularQueue.enQueue(4); // 返回 true
circularQueue.Rear(); // 返回 4
提示:
所有的值都在 0 至 1000 的范围内;
操作数将在 1 至 1000 的范围内;
请不要使用内置的队列库。
动图演示
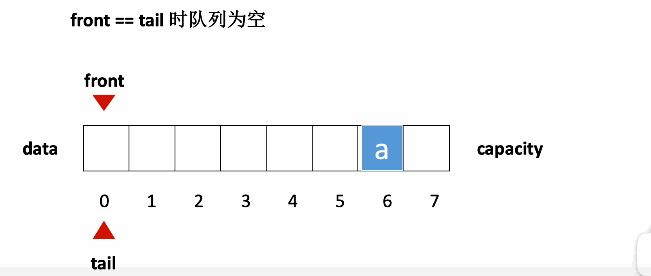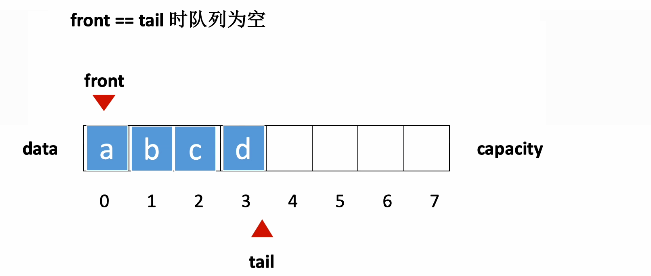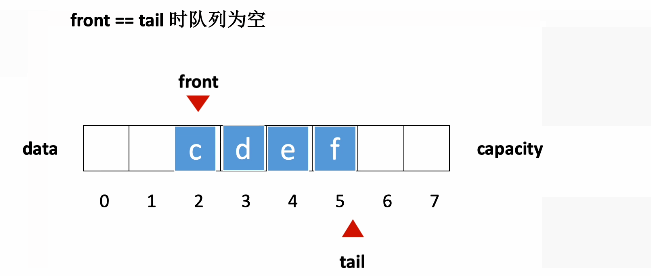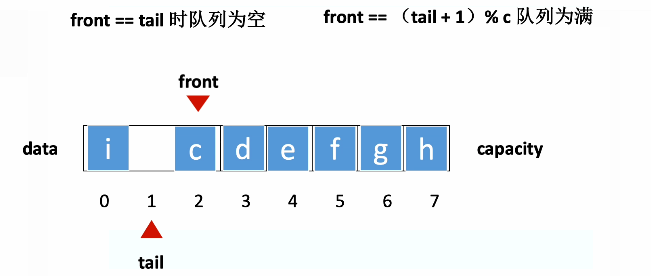
(动图来自 https://blog.csdn.net/qq_42996461/article/details/125674149)
实现容量为k的循环队列,可以定义一个大小为k的动态数组。同时,也可以通过链表实现。本文通过动态数组vector实现,并且在此过程中不使用指针。变量的定义与解释如下:
private:
vector<int> queue; //循环队列
int front; //队首
int rear; //队尾
int capacity; //队列的容量对于使用指针实现容量为k的循环队列,需要定义(k+1)的空间,用于判空判满。但如果不使用指针实现,只需定义k的空间即可。
验空与验满
由于存入队列的值的大小在0-1000之间,因此我们可以在队列初始化以及删除元素时用-1来代替数组中元素为空的情况。所以在验空和验满时,只需要判断数组中是否 全部元素为-1 或者 全部元素不为-1 来实现。
bool isEmpty() {
for (int cptime = 0; cptime < capacity; cptime++)
{
if (queue[cptime] != -1)
{
return false;
}
}
return true;
}
bool isFull() {
for (int cptime = 0; cptime < capacity; cptime++)
{
if (queue[cptime] == -1)
{
return false;
}
}
return true;
}入队
在进行入队操作时,首先应该考虑队列是否已满,如果队列已满,那就无法进行入队操作,直接返回false即可。再考虑队尾是否处在数组的末尾,如果是这样的话,那就应该在数组的头部插入数据,并且将队尾指向数组的头部。如果不在数组的末尾,那么按顺序插入即可。
bool enQueue(int value) {
if (isFull() == true)
{
return false;
}
if (rear == capacity - 1)
{
rear = 0;
queue[rear] = value;
return true;
}
queue[rear+1] = value;
rear++;
return true;
}由于队列遵循先入先出原则。因此在“再考虑队尾是否处在数组的末尾,如果是这样的话,那就应该在数组的头部插入数据,并且将队尾指向数组的头部。”的时候时,不需要考虑数组的头部是否有数据。因为对于队列来说,只会出现一种“队首和队尾都有数据,而队尾的指针指向数组的末尾”的情况,那就是队列已满。但由于在入队时我们优先考虑了队列是否已满的情况,所以在此步就不需要考虑了。
出队
出队的逻辑与入队相似。
bool deQueue() {
if (isEmpty() == true)
{
return false;
}
if (front == capacity - 1)
{
front = 0;
queue[capacity-1] = -1;
return true;
}
queue[front] = -1;
front++;
return true;
}取出队首/队尾数据
只需要获取front或者rear指向的数据即可。(由于题目没有要求,因此本代码未考虑当队列为空的情况)
int Front() {
if (isEmpty() == true)
{
return -1;
}
return queue[front];
}
int Rear() {
if (isEmpty() == true)
{
return -1;
}
return queue[rear];
}
最终代码
class MyCircularQueue {
private:
vector<int> queue;
int front;
int rear;
int capacity;
public:
MyCircularQueue(int k) {
queue.resize(k);
front = 0;
rear = -1;
capacity = k;
for (int cptime = 0; cptime < k; cptime++)
{
queue[cptime] = -1;
}
}
bool enQueue(int value) {
if (isFull() == true)
{
return false;
}
if (rear == capacity - 1)
{
rear = 0;
queue[rear] = value;
return true;
}
queue[rear+1] = value;
rear++;
return true;
}
bool deQueue() {
if (isEmpty() == true)
{
return false;
}
if (front == capacity - 1)
{
front = 0;
queue[capacity-1] = -1;
return true;
}
queue[front] = -1;
front++;
return true;
}
int Front() {
if (isEmpty() == true)
{
return -1;
}
return queue[front];
}
int Rear() {
if (isEmpty() == true)
{
return -1;
}
return queue[rear];
}
bool isEmpty() {
bool sum = true;
for (int cptime = 0; cptime < capacity; cptime++)
{
if (queue[cptime] != -1)
{
sum = false;
break;
}
}
return sum;
}
bool isFull() {
bool sum = true;
for (int cptime = 0; cptime < capacity; cptime++)
{
if (queue[cptime] == -1)
{
sum = false;
break;
}
}
return sum;
}
};
动态拓展队列空间与链表实现
详情见2019计算机考研408数据结构大题。
【2019统考真题】请设计一个队列,要求满足:①初始时队列为空;②入队时,允许增加队列占用空间;③出队后,出队元素所占用的空间可重复使用,即整个队列所占用的空间只增不减;④入队操作和出队操作的时间复杂度始终保持为O ( 1 ) O(1)O(1)。请回答下列问题:
1)该队列是应选择链式存储结构,还是应选择顺序存储结构?
2)画出队列的初始状态,并给出判断队空和队满的条件。
3 ) 画出第一个元素入队后的队列状态。
4)给出入队操作和出队操作的基本过程。
如果使用动态数组实现的话,可以使用 resize 方法拓展空间。但对于本题要求的链表实现,可以见 https://blog.csdn.net/qq_50710984/article/details/113946205